Chromatische Dispersion
Was steckt dahinter?
Die Datenübertragung über Glasfaserleitungen ist zwar deutlich weniger fehleranfällig wie noch die alten Kupferleistungen des Festnetzes. Dennoch gibt es einige physikalischen Effekte, welche auch hier die Signalqualität negativ beeinflussen können. Eine davon ist die sogenannte chromatische Dispersion. Alles zur Bedeutung und den Grundlagen hier.
Was versteht man unter der chromatischen Dispersion?
Neben der Signaldämpfung in Glasfaserleitungen, spielt auch die Berücksichtigung der Dispersion eine entscheidende Rolle für die Güte einer fiberoptischen Datenverbindung.Auch wenn der Name recht kompliziert klingen mag, liegt doch ein recht simpler physikalischer Effekt zugrunde. Bei Glasfasernetzen werden ja verschiedene Frequenzbereiche (Bänder) genutzt, welche sich in der Wellenlänge und somit Frequenz unterschieden - bildlich gesprochen in der Farbe.
Schickt man z.B. einen roten Lichtimpuls durch ein Glasfaserkabel, hat dieser eine kürzere Laufzeit bis zum Empfänger als ein blauer Lichtpuls. Die chromatische Dispersion beschreibt also die Zeitverzögerung zwischen zwei Wellenlängen auf eine bestimmten Distanz L. Wohlgemerkt nur in einem Medium wie Quarzglas (vulga Glasfaser) oder Luft. Denn im Vakuum ist die Lichtgeschwindigkeit immer exakt gleich groß mit c = 299.792,458 km/s.
Nun nutzt man bei Glasfaserkabeln verschiedene Bandbereiche. Durch den genannten Effekt laufen verschiedene Spektralkomponenten eines Pulses unterschiedlich schnell. Je größer die Distanz, desto weiter „zieht sich das Signal sozusagen auseinander“. Die so entstehende Pulsverbreiterung sorgt bei langen Strecken und hohen Bitraten zunehmend für Übertragungs- bzw. Bitfehler. Auch genannt „Inter-Symbol-Interference“.
In der Praxis misst die chromatische Dispersion, um wieviel Pikosekunden sich Licht unterschiedlicher Wellenlänge pro Nanometer Spektralbreite und Kilometer Glasfaserkabellänge in der Zeit auseinander divergiert [ps/(nm·km)]. Der Wert ist wichtig, um diesen dann bei Bedarf zu korrigieren. Mehr zur Berechnung später.
Einfaches Beispiel, wie die chromatische Dispersion entsteht
Nehmen wir eine Distanz von 10 Kilometern, was beim Glasfaserausbau durchaus schnell zusammen kommt. Die Deutsche Telekom hat bundesweit schon Fasern mit einer Gesamtlänge verbaut, die fast so groß ist wie die Distanz von der Erde zum Mond und zurück!
Für die Wellenlänge von rotem Licht nehmen wir 650 Nanometern an, Blau mit 450 nm.
Die Formel für die Lichtgeschwindigkeit in einem Glasfaserkabel (Silica-Einmoden-Faser) ist
λ = 650 nm (rot): ≈ 204 000 km/s → Laufzeit ≈ 49,0 µs
λ = 450 nm (blau): ≈ 202 000 km/s → Laufzeit ≈ 49,5 µs
Der blaue Lichtpuls ist also 0,5 Microsekunden schneller wie der rote.
PS: Ganz unten finden Sie noch einen Beispielrechner für die Zeitverzögerung.
Berechnen lässt sich zunächst die Gruppengeschwindigkeit mit folgender Formel:
steht dabei für die sogenannte Gruppengeschwindigkeit. Der Schnelligkeit, mit der sich die Energie bzw. das Puls-Maximum in der Faser fortpflanzt. Sozusagen das „Signal“, welches wir für eine Datenübertragung in der Glasfaser benötigen. Sie errechnet sich aus dem Quotienten der Lichtgeschwindigkeit c und dem Gruppenindex 
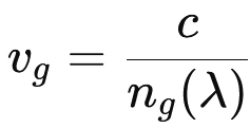
. Dieser berücksichtigt den Brechungsindex je Wellenlänge und wie schnell sich n mit der Wellenlänge ausbreitet.Den Gruppenindex findet man für Standardglasfasern direkt als Angabe im Hersteller‑Datenblatt oder berechnet ihn aus öffentlich verfügbaren Refraktiv‑Tabellen (Sellmeier‑Koeffizienten) mit
. In unserem Beispiel beträgt der Gruppenindex 1,464.
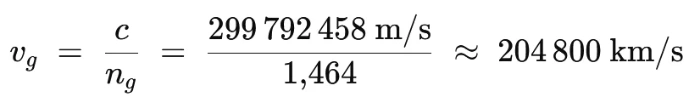
Zum Schluss muss für die Bestimmung der Laufzeit noch Weg durch Geschwindigkeit geteilt werden. Also unsere exemplarischen 10.000 Meter / . Das ergibt die Laufzeit (t).
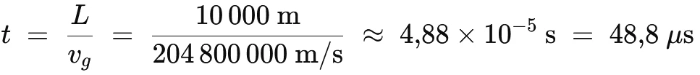
Man kann den Zusammenhang auch gut in einem Diagramm darstellen. Auf der X-Achse wird die Wellenlänge Lambda eingezeichnet. Y bildet die Gruppengeschwindigkeit in km/s ab. Bis ca. 1300 nm steigt die Kurve an, daher die Gruppengeschwindigkeit steigt. Mit kurzen Wellenlängen (z.B. blau) nimmt diese also erst einmal zu. Im Infrarotbereich flacht die Kurve ab ca. 1310 nm dann wieder ab. Der Wert für liegt hier ca. bei 204.000 – 205.000 km/s, was selbst bei hohen Laufstrecken nur sehr kleine Abweichungen und somit Dispersion bedeutet.
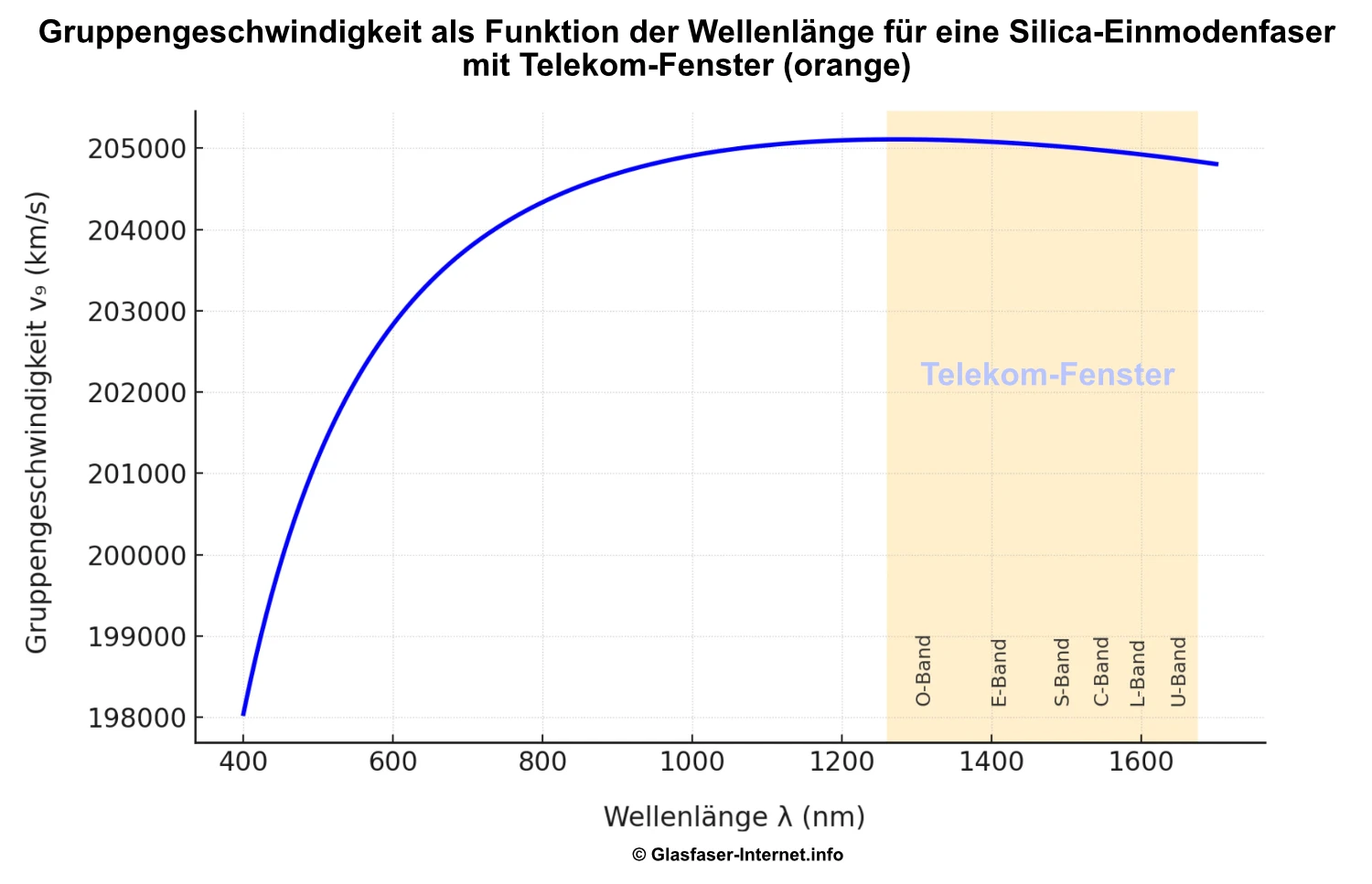
Was ist das „Telekom-Fenster“
In der oberen Grafik haben wir ein sogenanntes „Telekom-Fenster“ eingezeichnet. Zunächst einmal hat das nichts mit der Deutschen Telekom zu tun. Vielmehr bezeichnet es den Wellenlängenbereich, in denen Glasfasern typischer Weise besonders geringe Dämpfungseigenschaften aufweisen. Daher wird dort bevorzugt Glasfaser-Internet eingesetzt.
Denn: Je geringer die Dämpfung, desto kleiner fällt der Signalverlust pro Wegeinheit aus. In der Praxis sind diese Fenster in 6 Bändern definiert. Diese Frequenzbereiche werden für die Informationsübertragung über fiberoptische Kabel genutzt. Idealer Weise verläuft im „Telekom-Fenster“ die Gruppengeschwindigkeit sehr flach und somit ist auch die chromatische Dispersion gering.
Berechnung der chromatischen Dispersion
Die eigentliche Berechnung ist relativ kompliziert und es gibt mehrere Ansätze. Vom Prinzip her handelt es sich um die zweite Ableitung der Laufzeit in Bezug auf die Wellenlänge. Wir wollen hier die c.D. weiter über den Gruppendelay
und Gruppenindex
definieren. Dann ergibt sich die chromatische Dispersion aus:
Ein weiterer Weg führt über den effektiven BrechungsIndex. In der Praxis bedient man sich allerdings eher Näherungs-Faustformeln, da die genaue Ableitung des Brechungsindex kompliziert ist. Einer der Nährungen ist die bekannte Sellmeier-Gleichung.
Die beiden Koeffizienten Bi, Ci sind dabei materialabhängig und sind u.a. für Quarzglas bekannt.
Noch einfacher geht es über die Näherung für Standard Singlemode-Faser nach ITU-T G.652. Dafür benötigt man vier Variablen:
λ0: Null‑Dispersion‑Wellenlänge der Faser (bei Standard‑SMF ≈ 1310 nm)
S0: Dispersion‑Slope‑Konstante: Stärke der Änderung von D(λ) pro Wellenlängeneinheit
S0/4: Skalierungsfaktor aus der Taylor‑Entwicklung des Dispersion‑Spektrums um λ0
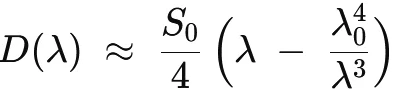
In der Regel werden aber Messwerte, Tabellenwerte oder Herstellerangaben für D verwendet, da dieses Vorgehen praxisnäher ist.
Was ist die Null‑Dispersion?
Hierbei handelt es sich um eine spezifische Wellenlänge, bei der sich die chromatische Dispersion aufhebt bzw. Null wird. Das Licht verschiedener Wellenlängen breitet sich dann also praktisch gleich schnell aus und mögliche Signalverzerrungen werden vermieden. Bei Standard-Glasfasern (Singlemode fiber) liegt der Null-Dispersionspunkt bei zirka 1310 nm. Moderne Glasfaserkabel (Non-Zero Dispersion Shifted Fiber) können diesen Punkt aber auch in Richtung eines gewünschten Frequenzbandes verschieben, etwa bei 1530 nm. Denn dort ist die Dämpfung (Signalverlust mit steigender Entfernung) am geringsten (C-Band).Zeitverzögerung durch chromatische Dispersion (D)
Wenn D bekannt ist, lässt sich die Zeitverzögerung mit unserem Rechner hier leicht berechnen. Sie benötigen nur noch die spektrale Breite. Diese wird vom Hersteller der Laserdioden mit Full Width at Half Maximum (FWHM) angegeben. Sie entspricht der Differenz zwischen den beiden Wellenlängen, wenn die Intensität der Diode auf 50 % des Maximums gesunken ist.
Laufzeitverzögerung durch chromatische Dispersion
Δt = D × Δλ × K
Hinweis: Der Einfachheit halber haben wir uns in diesem Ratgeber nur Single-Mode berachtet. Es gibt aber auch Kabel bei denene mehrere Moden gleichzeitig übertragen werden können. Also Sigale mit verschiedenen "Ausbreitungswege" im Kabel. Mehr dazu hier über Multi-Mode Glasfaserkabel.
auch interessant:
» Was ist das Quanteninternet und worin liegt die Bedeutung?» Wie hoch sind die GF-Anschlusskosten für ein Haus?
» Was sind optische Fenster?
» Was ist Wavelength Division Multiplexing?
