Bei der Übertragung von Lichtsignalen in Glasfaserkabeln, kann es je nach Frequenzbereich zur sogenannten chromatischen Dispersion kommen. Mit diesem Tool können Sie diese berechnen und grafisch darstellen (plotten).
Der interaktive Rechner erlaubt zunächst das Einstellen eines bestimmten Wellenlängenbereiches, zum Beispiel konkret für das C-Band oder jeder anderen Konfiguration. Als nächstes lässt sich festlegen, ob die Darstellung des Dispersionsgraphen normal dezimal oder exponentiell erfolgen soll.
Auch die Wahl typischer Materialen ist möglich. Voreingestellt ist ein handelsübliche Standard‑Single‑Mode‑Glasfasern (z. B. Corning SMF‑28) mit typischen B‑ und C‑Koeffizienten. Bei Bedarf lassen sich aber auch andere Sellmeier-Parameter für eigene Kabel verwenden.
Der erste Graph plottet exemplarisch für die ersten beiden Materialen den Brechungsindex des Glases n(λ) als Funktion der Vakuum‑Wellenlänge λ. Der Wert n zeigt also, um welchen Faktor das Licht im Glas langsamer läuft im Vergleich zum Vakuum. Kürzere Wellen (z. B. 1300 nm) haben ein etwas höheres n wie längere Wellen mit 1600 nm. Aus n(λ) lässt sich die Gruppengeschwindigkeit ableiten, welche direkt für die Dispersion D (Pulse Broadening) verantwortlich ist.
Der n(λ)-Graph zeigt also, wie stark und in welcher Richtung das Material Licht bei verschiedenen Wellenlängen bricht. Die erste Ableitung davon steuert die Gruppenlaufzeit, während die 2. Ableitung

die Dispersion D(λ) steuert. Sprich, wie intensiv der Lichtpuls in der Faser über den Weg zeitlich auseinanderläuft. Im zweiten Graph ist dann der abgeleitete Dispersionsparameter zu sehen. Also die Gruppengeschwindigkeitsdispersion. Sie zeigt, um wie viele Pikosekunden sich ein Puls pro Nanometer Spektralbreite und pro Kilometer Faser ausbreitet.
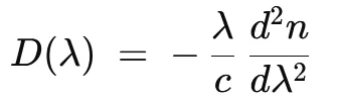
Die chromatische Dispersion beschreibt die Wellenlängenabhängigkeit der Gruppengeschwindigkeit (bzw. Phasengeschwindigkeit) in einem konkreten Medium (wie Glas). Anders als im Vakuum, führt die Ausbreitung der Pulse über größere Distanzen zu einer Verschiebung einzelner Frequenzkomponenten. Damit auch zur Pulsverbreiterung und schlussendlich zur Signalverzerrung.